辺ADと辺BCが平行な台形ABCDがあります。この台形の面積は108cm2です。
AD:BC=1:2で、点Eと点Fはそれぞれ辺ADと辺ABの真ん中の点です。右の図のように、点GはBEとCFの交わった点です。
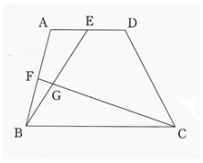
(1) FG:GCを求めなさい。
(2) 四角形CDEGの面積を求めなさい。
(解説と解答)
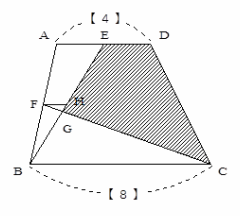
(1)
FからBCに平行に線を引き、BEとの交点をHとします。
AD:BC=1:2なので便宜上BC=【8】とするとAD=【4】AE=【2】
FHはAF:FB=1:1なのでFH=【1】よって三角形FGHと三角形GBCの相似からFG:GC=1:8
(2)
全体が108㎝2ですから三角形ABCは108×2/3 =72㎝2です。
AF:FB=1:1より三角形FBC=72÷2=36㎝2
FG:GC=1:8より三角形GBC=36×8/9 =32㎝2
三角形AEB=108×1/3 ÷2=18㎝2
したがって斜線部は108-32―18=58 (答え)58㎝2