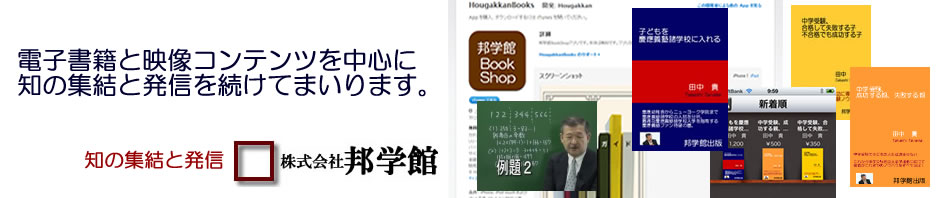
下の図で、点Eは直線AB上にあり、AE:EB=2:3
また三角形AEDと三角形EBCはともに正三角形です。
三角形DECの面積が36㎝2のとき、
四角形ABCDの面積を求めなさい。
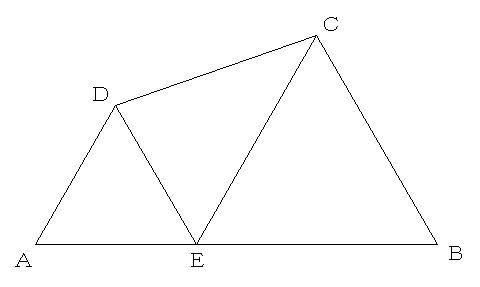
相似形になっていますので、二つの正三角形の面積比は2×2:3×3=4:9になっています。
ここで、AからCに線を引き、直線DEとの交点をPとします。
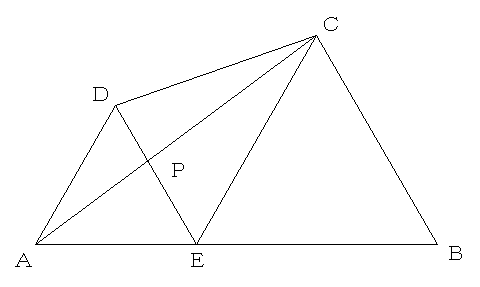
三角形ADPと三角形PECはADとECが平行なので、相似です。
このときAP:PC=2:3(=AD:EC)
したがって三角形ADEの面積は36×2/3=24㎝2
三角形ECBの面積は24×9/4=54㎝2
となるので、四角形ABCDの面積は24+36+54=114㎝2
となります。