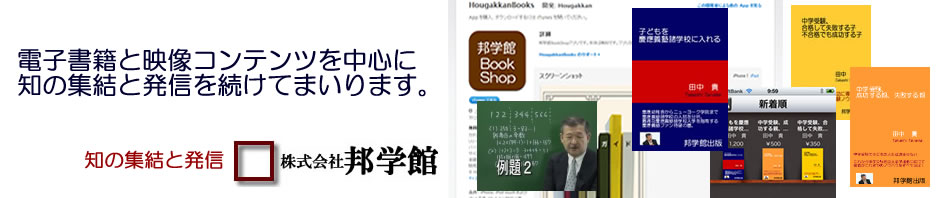
図のように1辺の長さが10㎝の正方形ABCDの頂点Bから発射した玉が、正方形の辺上の点、P、Q、R、S、T、U、・・・・で反射して、正方形の4つの頂点のいずれかに当たった時に止まるものとします。AR=4㎝のとき
(1)BUの長さは( )㎝です。
(2)斜線部の面積は( )㎝2です。
(3)玉は頂点( )で止まります。
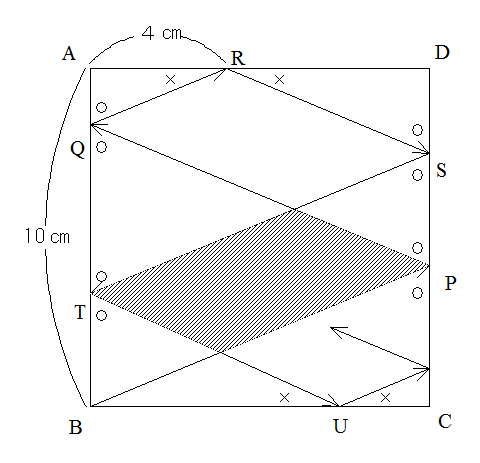
ボールを打ち出して、反射させる。繰り返し反射して、頂点に来たらボールが止まる。
このような問題は最近増えてきました。
いくつか考え方があるのですが、斜めの動きをたてとよこの動きに分解してみましょう。
玉がBを出発してRまで動くとき、横だけで見るとB→Pで10㎝、P→Qで10㎝ Q→Rで4㎝ 合計24㎝動いています。
この間に縦だけでは10㎝動くことになりますから、この斜めの線は合計するとたてに10㎝、横に24㎝動いているので、QA:AR=10:24=5:12になります。
(1)Bから出発した玉はUにつくまでにたてに20㎝動いていますから 20×12/5=48㎝ 横に動きます。
48÷10=4・・・8㎝ですから横に2往復したあと8㎝動くので、BU=8㎝になります。
(2)
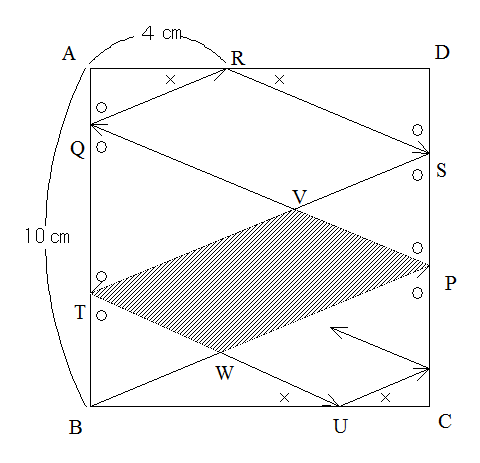
図のようにTSとQPの交点をVとします。TSとBPは平行ですからTB=SP=8×5/12=10/3
QBは横に20㎝動いたたての長さですから20×5/12=25/3 QT=25/3ー10/3=15/3よりTV:VS=3:2
なので、斜線部は平行四辺形TBPSの3/5になりますから
10/3×10×3/5=20㎝2になります。
(3)12と10の最小公倍数は60なので、横に60㎝動くと縦には25㎝ 横に120㎝動けば、縦は50㎝になります。
ともに10の倍数動けばよいので、横に120㎝、縦は50㎝で頂点に来ます。横は120÷10=12回動き、たては50÷10=5回動きます。
たては奇数回動くと、AかDにきて、横が偶数回動くとAかBに来るので、答えはAになります。
反射の問題は、相似の三角形がたくさんできていきますが、この斜辺の動きをたての動きとよこの動きに分解することによって、解法が見つかることが多いので、この着想は覚えておくと役に立つでしょう。