2011年芝中学の問題です。
下図のように一辺の長さが12m、6㎝、3cmの正方形があります。
それぞれの正方形の対角線の交点をP、Q、Rとするとき、三角形PQRの面積は( )cm2です。
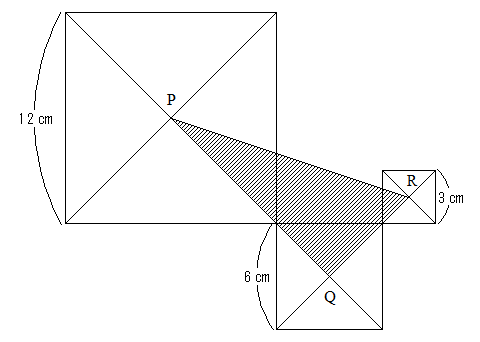
(解説と解答)
素朴に解くとすれば、台形から2つの三角形を引き、1辺6㎝の正方形の4分の1の三角形を加えるというやり方になるでしょうか。
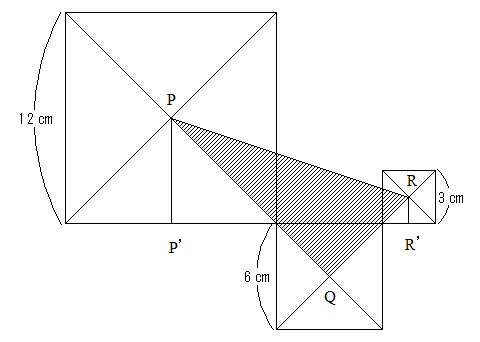
(1.5+6)×(6+6+1.5)÷2ー6×6÷2-1.5×1.5÷2+6×6÷4=50.625ー18-1.125+9=40.5
で答えが出ればよいのですが、こんな解き方もあるでしょう。
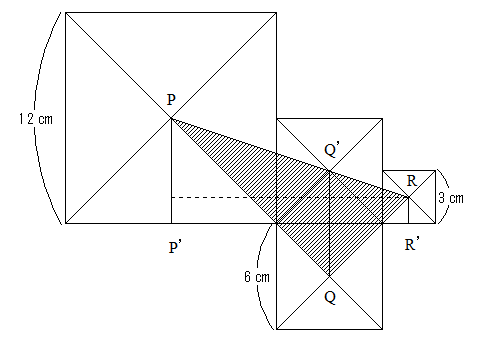
真ん中の正方形を折り返すと図のようになりますが、この中心のQ’はPR上を通ります。
PRはたて1、横3の直角三角形の斜辺ですがQ’Rもたて1.5㎝ よこ4.5㎝の直角三角形の斜辺です。
したがってQQ’は真ん中の正方形の1辺の長さと同じ6㎝ですから
P’R’=6+6+1.5より
13.5×6÷2=40.5と求めることができます。