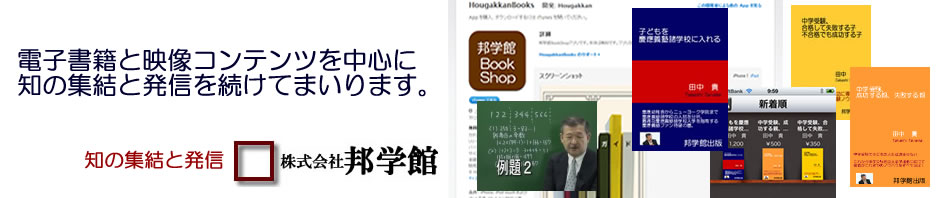
相似形の問題は、補助線を引いたり、図形を回転させてみたり、いろいろな方法を試していくことが大事です。
最近の入試問題はさらに進化して、単に補助線を引くだけではなく、分解して組み立てなおしたり、立体の中で平面を考えたりする問題が増えてきました。今から一気にそこまで能力を高めていくことは難しいので、段階的に問題を難しくするとしても、それぞれの段階でいろいろな見方を試していく、ということを実践していかなければならないでしょう。
まず最初に必要なことは、基本的な相似形を見つけることです。
三角形の相似形は一組の平行線から生まれます。代表的な三角形の相似のパターンは2つあります。
パターン1
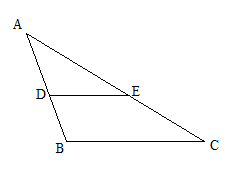
パターン2
この場合、直線BCと直線DEは平行で、したがって三角形ABCと三角形ADEは相似の三角形になります。これを問題のどこで見つけるか?ということが問題を解く鍵になります。
下の図で、BF:FEを求めなさい。
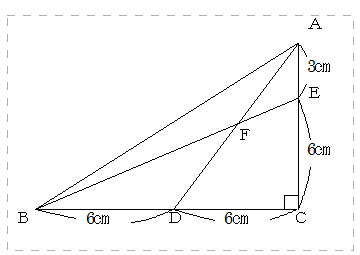
この問題の場合、
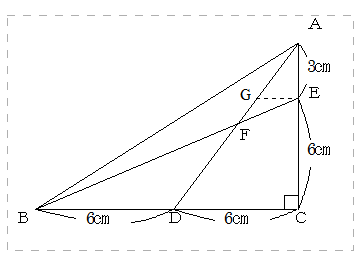
のようにEからBCに平行に線を引き、ADとの交点をGとすると
三角形AGEと三角形ADCの2つの三角形は上のパターン1の相似になり、AE:EC=1:2であることからGEの長さは6×1/3=2cm
とわかることになります。
そうすると三角形FBDと三角形FGEがパターン2の相似形になりますから、したがってBF:FE=6:2=3:1となるわけです。
図形をいろいろな角度から見て、補助線を引いたり、回転させたりしながら、この2つの相似形のパターンを見つける、というのは相似形を学習する一番最初のステップになります。そして、この理解がしっかりしてくると、いろいろな形に応用でき、図形の問題を解く力がどんどんついてくるのです。
最初からうまく解こう、などと考える必要はありません。
トライアンドエラーで、いろいろ試しながら解く力を培っていきましょう。
もちろん、ていねいに、じっくりと、とは「忘れずに」