下は慶應普通部の2012年の入試問題です。
太郎君は家から4kmはなれた公園に向かいました。家を出て毎分70mで20分歩いた所で、忘れ物に気がつき同じ速さで引き返しました。太郎君が家を出て16分後、お兄さんは自転車で家を出て太郎君の忘れ物を届けに行きました。太郎君は引き返してから4分後、お兄さんに出会いました。
(1) お兄さんは毎分何mの速さで届けに行きましたか。
(2)2人が出会った後、まだ忘れ物があったので、お兄さんは速さを毎分20m速めて、家にもどりすぐに太郎君を追いかけました。太郎君はお兄さんと別れてから、歩く速さを毎分10m速めて再び公園へ向かいました。お兄さんが太郎君に追いつくのは公園の何m手前ですか。
速さの問題は実際に、問題文が長いので条件を忘れてしまうことがあります。したがって題意をグラフに書いていくとわかりやすくなります。
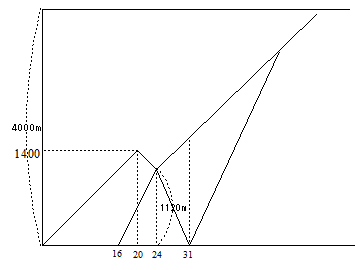
(1)20分歩いていたので70×20=1400m それから4分引き返しますので70×4=280 1400ー280=1120 お兄さんは24ー16=8分ですから、1120÷8=140m (お兄さんの分速)
(2)1120÷(140+20)=7分 したがってお兄さんは7分で戻ります。その間太郎君は70+10=80mの分速で7分進みます。 80×7=560m お兄さんと太郎君の間の距離は 1120+560=1680m 離れています。
1680÷(160ー80)=21分 160×21=3360 4000ー3360=640m 手前ということになります。
式を書くとこういう感じになりますが、やはりグラフをみながら確認していくと、今、何を出しているのか、間違えにくくなります。
速さの問題をグラフに書いてみる、という練習はしっかりやっていきましょう。