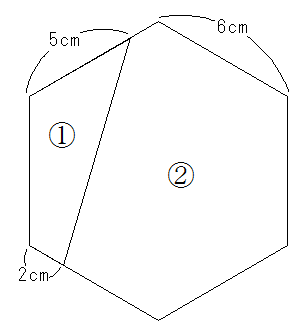
1辺の長さがすべて6㎝で、角がすべて等しい六角形を、直線で2つの部分に分けました。①の部分と②の部分の面積の比をもっとも簡単な整数の比で表すと、( ア ):( イ )になります。
正六角形は、6つの正三角形に分けることができるので、これを使います。ただ、①の左側に延長して同じような正三角形をつなげていきましょう。
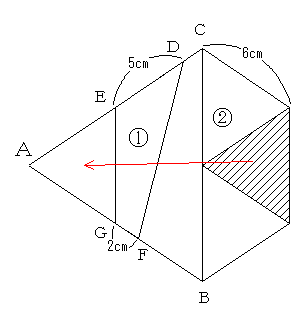
斜線の正三角形を【1】とすると、正六角形の面積は【6】
正三角形ABCの面積は【4】です。
三角形ADFは【4】の11/12×8/12=【22/9】になるので
そこから【1】を引いて①の面積は【22/9】ー 【1】=【13/9】
したがって②は【6】-【13/9】=【41/9】
①:②=13:41になります。
正六角形の問題の場合、構成する正三角形を使うと簡単に解けることが多いので、これもポイントとして覚えておいてください。