早稲田高等学院の問題
下図のように直方体の容器に水の入らない三角柱がはまっています。この容器を平らな床に置いて、毎分600mLの割合で水を入れたとき、6分45秒でいっぱいになりました。容器の厚さは考えないものをします。このとき、次の問いに答えなさい。
(1) 三角柱の高さを求めなさい。
(2) 太線でかかれた辺を床につけたまま、この容器を静かに45°傾けて水をこぼしてから元に戻しました。このとき水の水面の高さを求めなさい。
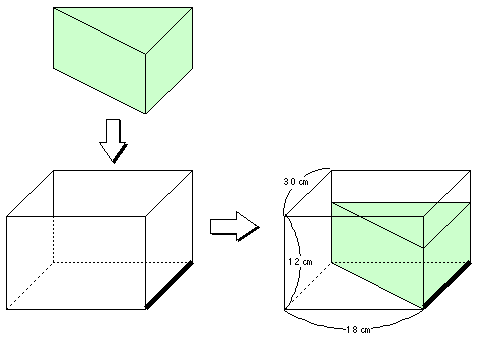
(1)
600×6 45/60=4050mLが水の体積です。容積は
30×12×18=6480mLですから三角柱の体積は
6480-4050=2430mL
三角柱の底面積は30×18÷2=270cm2ですから
2430÷270=9
(答え)9㎝
(2)
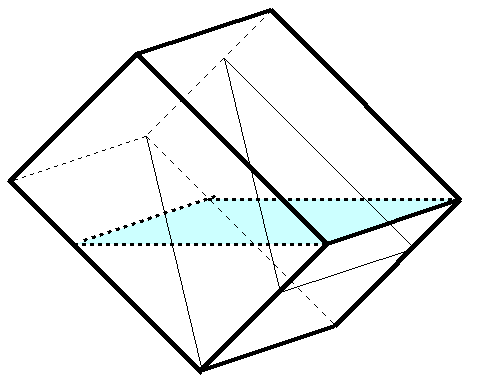 図1
図1
傾けると図のようになるわけです。水色の平面が水面ですね。そうすると水面よりも上の部分には水がいないわけです。しかし、三角柱があります。そこで三角柱がなかった場合をまず考えましょう。
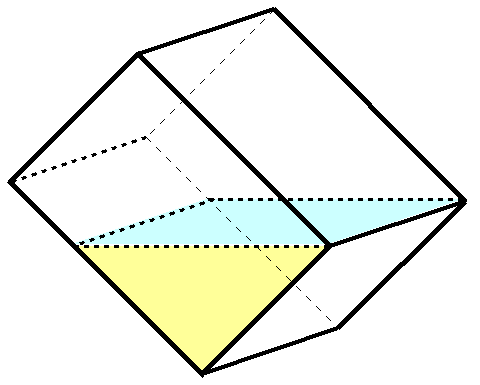 図2
図2
こうすると図の黄色い三角形は1辺が12㎝の直角二等辺三角形です。したがって水が入っていない部分は
6480-12×12÷2×30=4320㎝3あります。
しかし、ここに三角柱が入っているので、水色の平面の上にどのくらいの三角柱が入っているかを考えなければいけません。
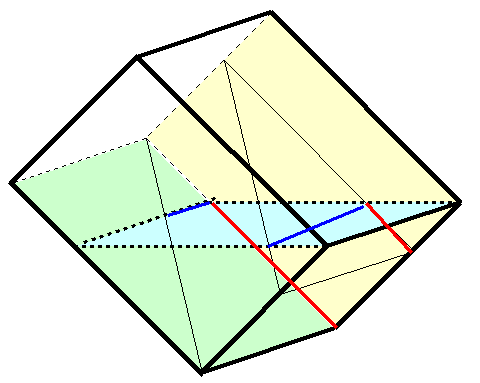 図3
図3
そこで図3の黄色の平面を見てみると、図4のようになっています。
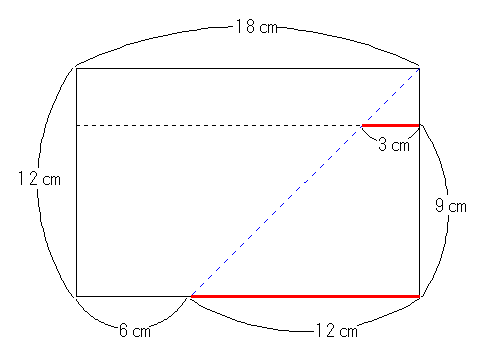 図4
図4
ここで赤い線は図3の赤い線と一致しているのに注意してください。図4の下の赤い線は12㎝になり。三角柱の高さは9㎝ですから、図の上の短い赤い線は3㎝になります。
今度は図3の緑の面を考えると図5のようになります。
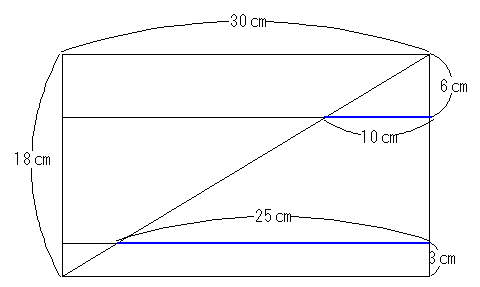 図5
図5
これも図3の青い線の部分が一致しています。
すなわち、水面上にある三角柱の部分は図6のような立体になっていることがわかります。
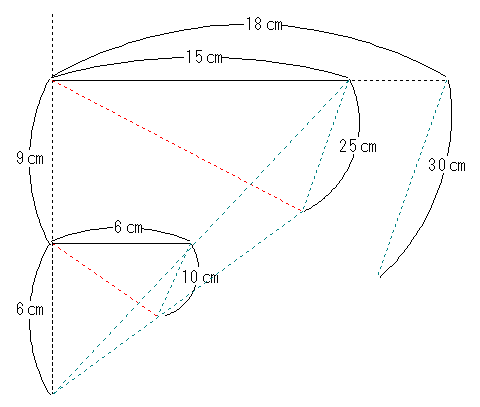 図6
図6
これは大きな三角柱から下の三角柱を引けばいいので、
15×25÷2×15÷3-6×10÷2×6÷3=937.5-60=877.5
したがって出た水の体積は
4320-877.5=3442.5 残っている水の体積は
4050-3442.5=607.5
になります。
高さ9㎝までの底面積は18×30÷2=270ですから
607.5÷270=2.25 (答え)2.25㎝